Tag: gravity

  • Einstein vs KFT: Two Paths to Understanding the Universe

    Einstein vs KFT: Two Paths to Understanding the Universe

    Introduction

    For more than a century, Albert Einstein and his General Theory of Relativity (GR) have shaped the way we think about gravity and the cosmos. Thanks to this framework, we can predict the motion of planets, study black holes, and even detect gravitational waves.

    But there is also a new perspective – TPK (Khandro Field Theory) – which interprets the same phenomena in a different and more direct way.

    Einstein: Spacetime as a Stage

    In Einstein’s view:

    • Gravity is not a force, but the curvature of spacetime.
    • Planets, photons, and particles move along “geodesics” – the straightest possible paths in this curved geometry.
    • Effects like the bending of starlight near the Sun or gravitational time dilation come directly from this curvature.

    It is an elegant but highly abstract framework: motion is dictated by the geometry of space and time itself.

    TPK: The Field Instead of Geometry

    TPK offers another picture:

    • The foundation is not curved spacetime but a real physical field – the Khandro Field.
    • This field has density and structure, and particles (including photons) respond to its gradients.
    • The elevator, rocket, or planet is simply a system moving through this field. Their motion does not change the photon’s path – the field does.

    In practice:

    • Where Einstein speaks of “spacetime curvature,” TPK speaks of a physical medium/field.
    • The trajectory of a photon depends only on the field, not on the motion of the observer.

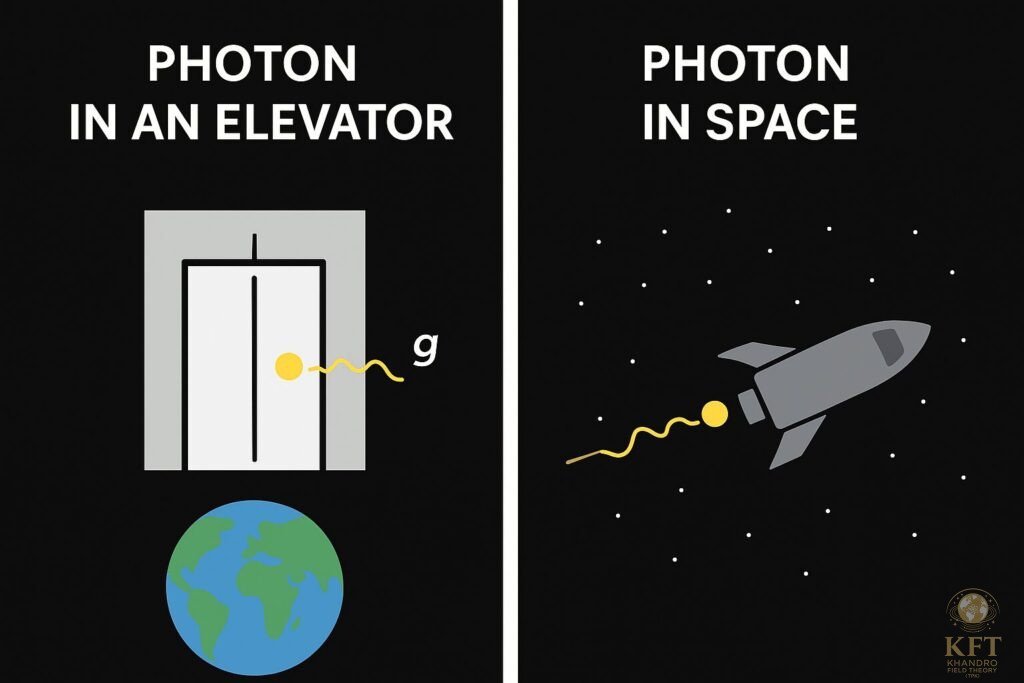
    Key Difference: A Photon in the Elevator

    • Einstein’s view: A photon in an accelerating elevator appears to curve toward the floor – an effect equivalent to gravity.
    • TPK’s view: The photon does not “follow the elevator.” Its path is determined only by the Khandro Field. The elevator is merely a moving measurement frame, with no influence on the photon’s trajectory.

    Agreement with Observations

    Both GR and TPK predict:

    • bending of light near massive bodies,
    • time dilation in gravitational fields,
    • extreme phenomena like black holes.

    The difference lies in interpretation:

    • Einstein – gravity as curved geometry,
    • TPK – gravity as the dynamics of a physical field.

    Conclusion

    History shows that great ideas can be described in different languages.
    Einstein gave gravity the language of geometry, while TPK gives it the language of a field.
    Both fit observations – but TPK offers a more intuitive, physical picture: light and matter always follow the field, not the observer’s motion.

  • Gravity – Newton vs KFT

    Gravity – Newton vs KFT

    In short: in Newton’s view, gravity is a force between masses. In KFT, we speak of a local reaction to the gradient of the field’s density — without “action at a distance.”

    Newton described gravity as a force acting between masses — mysteriously, “at a distance.” In his view, the Earth instantly affects every object within its reach. Although it was a revolutionary idea that explained planetary motion and falling bodies, the “force at a distance” itself remained an unresolved puzzle.

    KFT (Khandro Field Theory) introduces a different approach: instead of a “magical force,” it speaks of local interaction with the Khandro field. Space is filled with Khandro particles that cluster around matter. Large bodies, such as the Earth, push out and organize these particles, creating a denser gravitational field. An object in such a field is not “pulled from outside” but experiences interaction internally, at the level of its atoms.

    In practice, this means that KFT eliminates the need for action at a distance, providing a clear cause-and-effect: the greater the mass, the higher the field density, and therefore the stronger the interaction with surrounding objects. The “magic” of instantaneous action across infinite space disappears, replaced by a physical process — the interaction of matter with the external Khandro field. The field originates externally (e.g. from the Earth) but acts locally on each particle of matter inside the object. This opens a new way of looking at cosmic phenomena, from planetary motion to galactic dynamics.

    Gravity according to Newton

    Every body with mass attracts other bodies. The force grows with the masses and decreases with the square of the distance. We write it as: F = G \frac{m_1 m_2}{r^2}

    where F is the gravitational force, G is the gravitational constant, m_1 and m_2 are the masses of the bodies, and r is the distance between them.

    On Earth we get an acceleration of about: g \approx 9.81 ,\text{m/s}^2

    and planets orbit because gravity “pulls” them inward while their forward motion prevents them from falling straight down. The conceptual weakness is that in the classical version it looks like “action at a distance,” with a force that decreases like \propto 1/r^2.

    Gravity in KFT

    Instead of a force at a distance, we have an energy-density field (the Khandro field), and a body responds locally to the gradient of that density.

    The simplest expression is: a_r = – \frac{ \partial_r \rho_k }{ \rho_{kw}, \mathcal{K} }

    meaning that acceleration toward the “denser” region of the field is proportional to the local gradient (the derivative with respect to r), scaled by inertial constants.

    Intuitively: the apple falls because just “below it” the field is slightly denser than “above it”; a planet maintains orbit because the density profile around the Sun balances its forward motion.

    We gain full locality and causality (changes propagate at finite speed), and in simple conditions the numerical results match classical gravity; differences appear only in subtle effects.

    Numerical examples

    Newton (for comparison)

    • Near Earth’s surface:
      – free fall acceleration g \approx 9.81 ,\text{m/s}^2
      – force on 1 kg: F = mg \approx 9.81 , \text{N}
    • In low Earth orbit (~400 km altitude): g(r) = \frac{GM_\oplus}{r^2} ;;\Rightarrow;; g \approx 8.69 ,\text{m/s}^2

    Orbital velocity: v = \sqrt{\frac{GM_\oplus}{r}} \approx 7.67 ,\text{km/s}

    KFT – connecting it to numbers

    Assume the simplest density profile around a central mass: \rho_k(r) = (\rho_{kw,K}) , \frac{GM}{r}

    Then: \partial_r \rho_k = -(\rho_{kw,K}) , \frac{GM}{r^2} \Rightarrow a_r = -\frac{1}{\rho_{kw,K}} , \partial_r \rho_k = \frac{GM}{r^2}

    So in the simplest limit, KFT reproduces exactly what Newton’s law gives: a_r(r_\oplus) \approx g \approx 9.81 ,\text{m/s}^2

    and it still decreases as 1/r^2.

    If you introduce a subtle correction, e.g.: \rho_k(r) = (\rho_{kw,K}) , GM !\left(\frac{1}{r} + \varepsilon \frac{r}{R_\oplus^2}\right)

    then the relative change in acceleration is about: \frac{\Delta g}{g} \approx 2 \varepsilon

    This provides a simple “tuning knob” for precision tests.

    Summary

    Both pictures explain motion well, but the mechanisms differ:

    • Newton: “The Sun attracts the Earth by a force.”
    • KFT: “Around the Sun, the field density changes, and the Earth accelerates down the local gradient.”