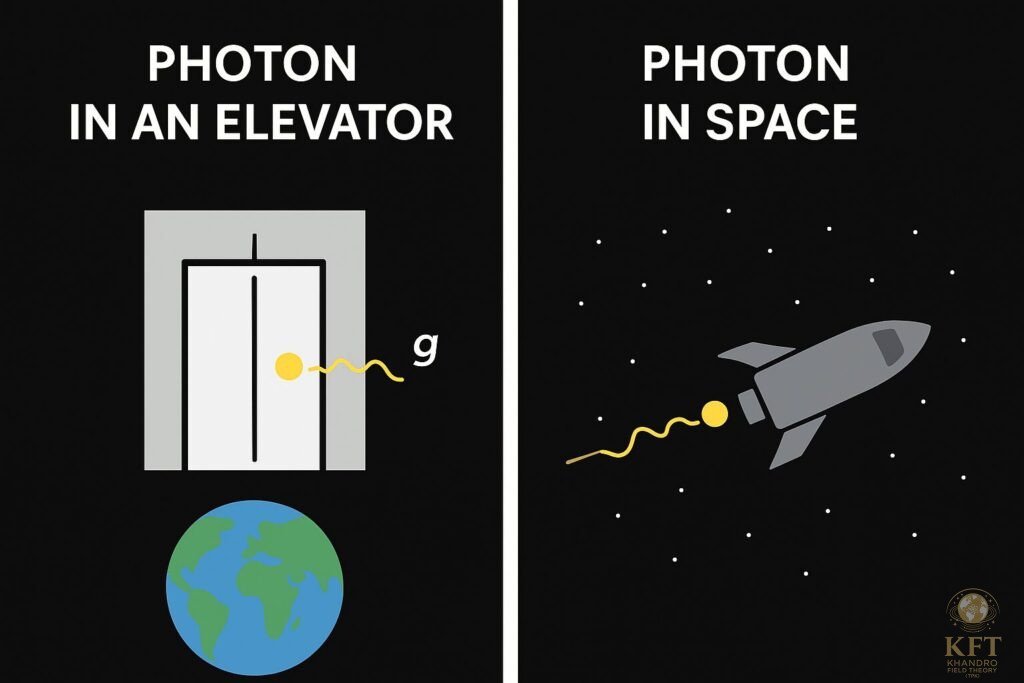
Teoria Prawa Khandro (TPK) zakłada, że pole khandro stanowi podstawową strukturę rzeczywistości. W tym ujęciu grawitacja oraz jej gradient wynikają nie z zakrzywienia czasoprzestrzeni, lecz z lokalnych różnic w gęstości pola khandro. Grawitacyjne oddziaływanie powstaje, gdy w jednorodnym polu pojawiają się obszary o większej gęstości, co wpływa na ruch cząstek i fotonów. Foton, przechodząc przez gęstsze obszary pola, ulega spowolnieniu, co prowadzi do obserwowanych efektów grawitacyjnych.
1. Uzasadnienie teoretyczne
Matematyczne równania TPK pokazują, że zmiany gęstości pola khandro odpowiadają klasycznym efektom grawitacyjnym, jakie opisuje mechanika Newtona i ogólna teoria względności. Jednak w odróżnieniu od tych podejść, TPK nie wymaga koncepcji zakrzywienia czasoprzestrzeni – wszystko można wyjaśnić poprzez własności pola khandro.
2. Uzasadnienie empiryczne
Istniejące dane obserwacyjne można interpretować w ramach TPK:
- Efekty pływowe i satelitarne: różnice w gęstości pola khandro odpowiadają różnicom w sile grawitacji obserwowanym przez satelity i sondy.
- Światło w polu grawitacyjnym: spowolnienie fotonu w obszarze gęstszego pola khandro daje efekt zbliżony do ugięcia światła przewidzianego w OTW.
- Fale grawitacyjne: można je interpretować jako dynamiczne zmiany gęstości pola khandro rozchodzące się w przestrzeni.
3. Możliwości weryfikacji eksperymentalnej
- Precyzyjne pomiary prędkości światła w silnych polach grawitacyjnych mogą wskazać, czy obserwowane opóźnienia da się tłumaczyć gęstością pola khandro.
- Interferometria kwantowa: badania nad wpływem pola grawitacyjnego na układy kwantowe mogą potwierdzić, że oddziaływanie pochodzi od zmiennej gęstości jednorodnego pola.
- Eksperymenty kosmologiczne: obserwacje rozchodzenia się światła w skali galaktycznej (soczewkowanie grawitacyjne, przesunięcia czasowe) mogą być interpretowane wprost jako efekt gęstości pola khandro.
4. Wnioski
TPK uzasadnia istnienie gradientu grawitacyjnego jako różnicę gęstości pola khandro, co daje alternatywne wyjaśnienie dla obserwowanych zjawisk grawitacyjnych. Dzięki temu teoria zachowuje zgodność z wynikami eksperymentów, a jednocześnie eliminuje konieczność wprowadzania zakrzywionej czasoprzestrzeni. Ostateczna weryfikacja TPK wymaga jednak precyzyjnych badań wpływu gęstości pola khandro na prędkość i tor światła.
Porównanie podejścia OTW i TPK do gradientu grawitacyjnego
| Aspekt | Ogólna Teoria Względności (OTW) | Teoria Prawa Khandro (TPK) |
|---|---|---|
| Źródło grawitacji | Zakrzywienie czasoprzestrzeni przez masę i energię | Zmiany gęstości pola khandro |
| Gradient grawitacyjny | Wynika z różnicy w zakrzywieniu przestrzeni w różnych punktach | Wynika z różnic w gęstości pola khandro w różnych punktach |
| Ruch fotonu | Foton podąża geodezyjną w zakrzywionej czasoprzestrzeni (pozorna zmiana toru) | Foton spowalnia w gęstszym polu khandro, co zmienia jego tor (efekt podobny do refrakcji) |
| Tłumaczenie ugięcia światła | Efekt krzywizny czasoprzestrzeni | Efekt spowolnienia fotonu w gęstszym polu |
| Fale grawitacyjne | Drgania zakrzywionej czasoprzestrzeni | Zmienne fluktuacje gęstości pola khandro rozchodzące się w przestrzeni |
| Matematyka | Równania tensora Einsteina | Równania opisujące dynamikę pola khandro |
| Weryfikacja eksperymentalna | Soczewkowanie grawitacyjne, przesunięcia czasowe, fale grawitacyjne | Pomiary zmian prędkości światła w polu grawitacyjnym, eksperymenty mikrograwitacyjne, interferometria kwantowa |
W skrócie:
- OTW mówi: grawitacja to geometria (zakrzywienie).
- TPK mówi: grawitacja to fizyka pola (gęstość khandro).