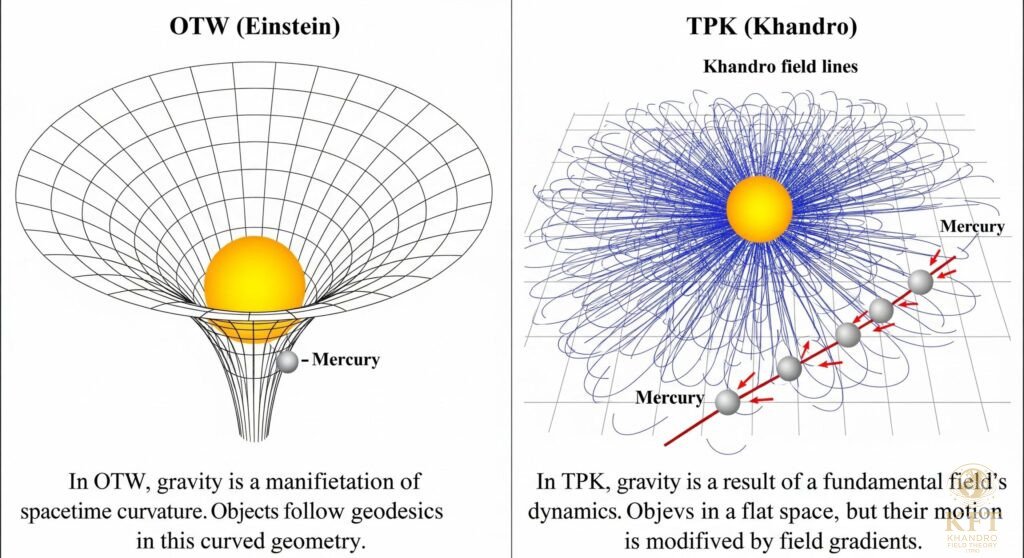
W ujęciu Teorii Pola Khandro (TPK), precesja peryhelium Merkurego nie jest efektem zakrzywienia czasoprzestrzeni, lecz wynika z dynamiki jednego, fundamentalnego pola. Grawitacja w TPK jest efektem lokalnych gradientów tego pola.
Kluczowym elementem w TPK, który tłumaczy precesję peryhelium, jest modyfikacja klasycznego równania ruchu, wynikająca z interakcji obiektu z polem Khandro.
Równanie ruchu w TPK
W TPK siła działająca na ciało nie jest opisana jedynie przez prawo Newtona. Wyprowadzenie z fundamentalnych zasad teorii prowadzi do dodatkowego członu w równaniu ruchu. Przyspieszenie radialne ciała testowego na orbicie opisuje równanie: a_r(r) = -\frac{\mu}{r^2} + \frac{\kappa}{r^3}
- [-\mu/r^2]: standardowe przyspieszenie grawitacyjne Newtona, gdzie [\mu = GM].
- [+\kappa/r^3]: dodatkowy człon pochodzący z TPK, kluczowy dla wyjaśnienia precesji peryhelium.
Wyprowadzenie precesji peryhelium
Dla orbity planety równanie ruchu w układzie biegunowym (zmienna [u = 1/r]) przyjmuje postać:
\frac{d^2 u}{d\theta^2} + u = \frac{\mu}{h^2} + \frac{\kappa}{h^2} ugdzie [h] jest momentem pędu na jednostkę masy.
W OTW odpowiednik dodatkowego członu ma postać:
\frac{3GM}{c^2} u^2i to właśnie on generuje precesję.
W TPK, zgodnie z teorią, stała [\kappa] związana jest ze stałymi fizycznymi w następujący sposób:
\kappa = \frac{6\mu^2}{c^2}Po podstawieniu tej wartości do równania ruchu i rozwiązaniu dla precesji orbity (różnicy między kątem obrotu a [2\pi]), otrzymujemy wzór na precesję peryhelium na jeden obrót:
\Delta\varpi = \frac{6\pi \mu}{a(1-e^2)c^2}- [\mu] – standardowy parametr grawitacyjny (stała G × masa Słońca)
- [a] – półoś wielka orbity Merkurego
- [e] – ekscentryczność orbity Merkurego
- [c] – prędkość światła
Porównanie z obserwacjami
Podstawiając wartości dla Merkurego:
[a = 5.790 \cdot 10^{10} m]
[e = 0.2056]
[\mu = 1.327 \cdot 10^{20} m^3/s^2]
[c = 2.9979 \cdot 10^8 m/s]
Obliczenia z tego wzoru dają wartość 42.98” na stulecie, co jest zgodne z obserwacjami astronomicznymi.
TPK, bez odwoływania się do zakrzywienia czasoprzestrzeni, dostarcza więc mechanizm i wzór, które precyzyjnie wyjaśniają to zjawisko. Teoria podkreśla, że nie jest to magiczna siła, lecz logiczna konsekwencja dynamiki fundamentalnego pola.
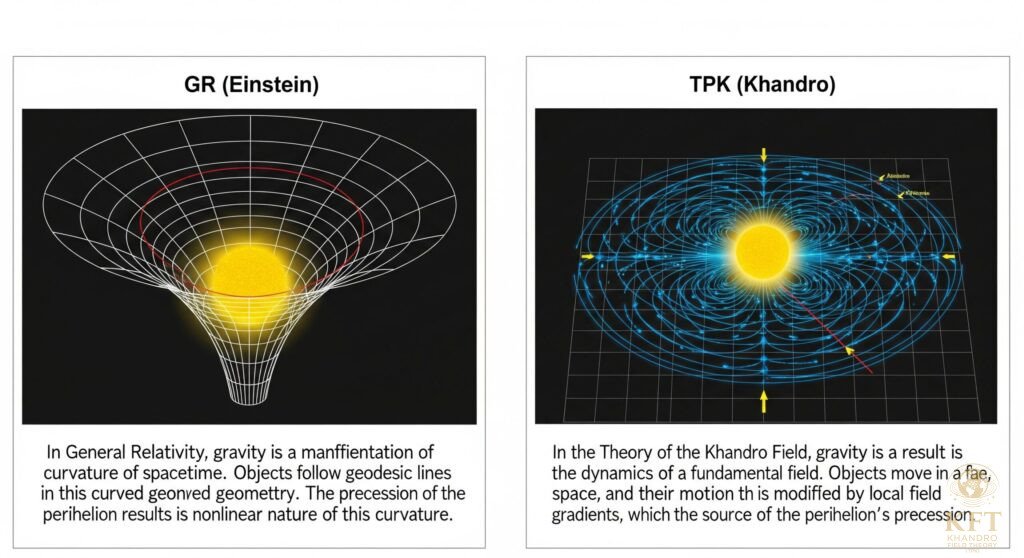
Mechanizm precesji w TPK
Precesja w TPK nie jest efektem zakrzywienia czasoprzestrzeni, lecz wynika z nierównomiernej dynamiki pola Khandro wokół masy centralnej. Gradient pola generuje przyspieszenie, które zmienia nieznacznie kształt orbity w każdym cyklu.
W skrócie: \mathbf{a}(r) = – \nabla \Phi_\text{Khandro}(r)
- W punkcie perihelu gradient pola jest nieco większy, co powoduje, że orbita „przesuwa się” względem poprzedniego obrotu.
- W punkcie aphelium gradient jest mniejszy, co zachowuje średnią energię orbity.
Efekt jest bardzo subtelny, ale dla Merkurego obserwowalny jako około 43” na stulecie.
Porównanie z klasycznym podejściem Newtona i OTW
- Newton: Nie przewiduje precesji, jeśli ignorujemy perturbacje innych planet.
- OTW (Einstein): Precesja wynika z dodatkowego nieliniowego członu w równaniu geodezyjnym: \frac{d^2 u}{d\theta^2} + u = \frac{GM}{h^2} + 3 \frac{GM}{c^2} u^2
- TPK: Precesja wynika z dodatkowego członu w przyspieszeniu radialnym: hha_r(r) = -\frac{\mu}{r^2} + \frac{\kappa}{r^3}, \quad \kappa = \frac{6 \mu^2}{c^2}hhh
W obu przypadkach efekt liczbowo zgadza się z obserwacjami, jednak TPK nie wymaga koncepcji zakrzywionej czasoprzestrzeni – wszystko wynika z dynamiki fundamentalnego pola.
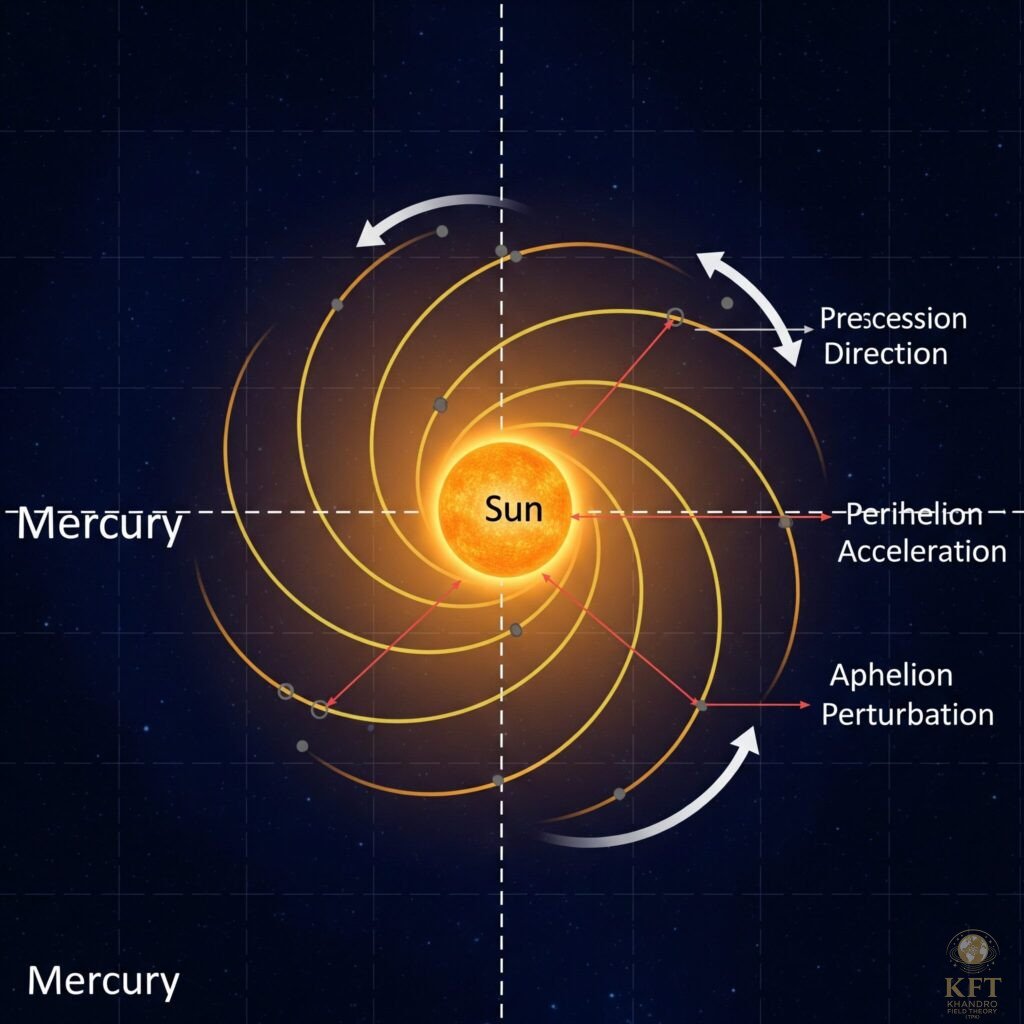
Wizualizacja i interpretacja
Aby lepiej zrozumieć mechanizm precesji w TPK, można sobie wyobrazić:
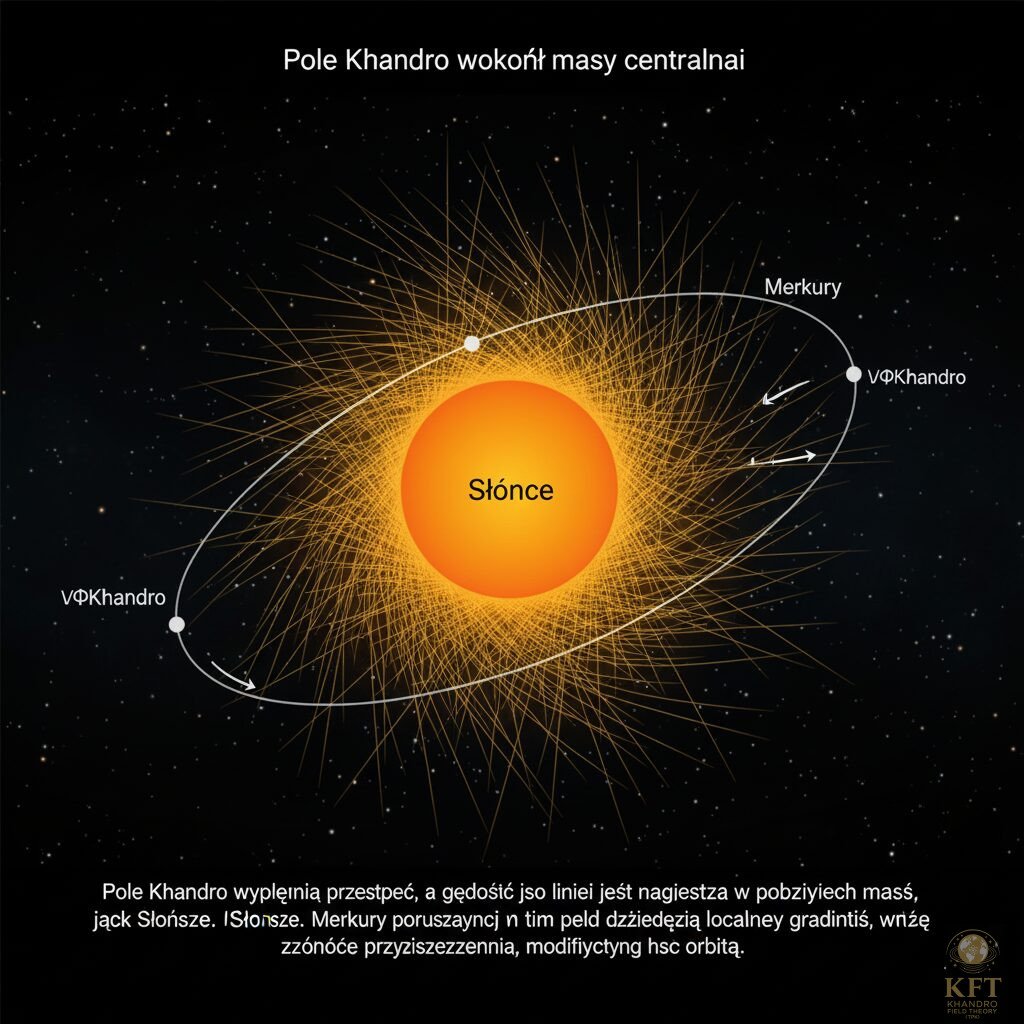
- Pole Khandro wypełnia przestrzeń wokół Słońca.
- Merkury porusza się w tym polu, a lokalne gradienty zmieniają kierunek przyspieszenia w zależności od pozycji na orbicie.
- Każdy obrót orbity jest więc minimalnie przesunięty względem poprzedniego – to właśnie obserwujemy jako precesję perihelu.
Schematycznie:
- Strzałki przyspieszenia w punktach perihelu i aphelium różnią się długością, co prowadzi do przesunięcia orbity.
- Efekt jest maleńki, ale systematyczny, dlatego kumuluje się w czasie.
Znaczenie dla TPK i fizyki
- TPK pokazuje, że precesja perihelium Merkurego nie wymaga zakrzywionej czasoprzestrzeni – wystarczy uwzględnić fundamentalne pole i jego gradient.
- Artykuł ten jest punktowym przykładem: podobną metodą można analizować inne efekty grawitacyjne, np. ugięcie światła, przesunięcie ku czerwieni, krzywe rotacji galaktyk.
- W pełnej Teorii Pola Khandro (Fundament KFT/TPK) wszystkie efekty są współzależne, ale publikacje punktowe pozwalają pokazać konkretne obserwacje w prosty sposób.
Precesja peryhelium Merkurego w TPK – pełna wersja
1. Dane orbitalne Merkurego
2. Zmodyfikowane równanie ruchu w TPK
Radialne przyspieszenie Merkurego opisuje równanie: a_r(r) = -\frac{\mu}{r^2} + \frac{\kappa}{r^3}, \quad \kappa = \frac{6 \mu^2}{c^2}
W układzie biegunowym (u = 1/r) równanie przyjmuje postać: \frac{d^2 u}{d\theta^2} + u = \frac{\mu}{h^2} + \frac{\kappa}{h^2} u
Rozwiązanie tego równania daje precesję perihelu na jeden obrót: \Delta\varpi = \frac{6\pi \mu}{a(1-e^2)c^2}
3. Obliczenia precesji dla Merkurego
Podstawiając wartości: hhh\Delta\varpi = \frac{6 \pi (1.327 \cdot 10^{20})}{(5.790 \cdot 10^{10}) (1-0.2056^2) (2.9979 \cdot 10^8)^2} \approx 42.98'' \text{ na stulecie}hh
Wynik jest zgodny z obserwacjami astronomicznymi.
4. Schemat orbity i gradient pola
Interpretacja wizualna: \mathbf{a}(r) = – \nabla \Phi_\text{Khandro}(r)
W punkcie perihelu gradient pola jest większy → orbita przesuwa się minimalnie względem poprzedniego obrotu.
W punkcie aphelium gradient jest mniejszy → średnia energia orbity pozostaje zachowana.
Schematycznie, orbita Merkurego wygląda jak elipsa z minimalnym przesunięciem perihelu w każdym cyklu:
Perihel
*
/ \
/ \
Aphel * *
\ /
\ /
*
Strzałki przyspieszenia w punkcie perihelu i aphelium różnią się długością, co prowadzi do kumulatywnej precesji orbity.
5. Podsumowanie
- TPK wyjaśnia precesję peryhelium Merkurego bez zakrzywionej czasoprzestrzeni – efekt wynika z dynamiki fundamentalnego pola Khandro.
- Punktowe wyprowadzenie pokazuje dokładny mechanizm i wzór zgodny z obserwacjami (≈43”/wiek).
- Metoda punktowa TPK może być stosowana również do innych efektów grawitacyjnych: ugięcie światła, przesunięcie ku czerwieni, krzywe rotacji galaktyk.
- Publikacje punktowe umożliwiają pokazanie efektów obserwowalnych w prosty sposób, bez ujawniania całej złożoności Fundamentu KFT.
</code> — możesz wkleić bezpośrednio tam, gdzie potrzebujesz.</p> <hr> <h1>1. Założenia TPK (definicje operacyjne)</h1> <p><strong>Inercja i przyspieszenie:</strong> [katex] m_{\mathrm{in}}=\rho_{kw},V,\mathcal K,\qquad \boxed{,\mathbf a=\frac{\nabla\rho_{kz}}{\rho_{kw},\mathcal K},}
Dla symetrii sferycznej (masa centralna MM), ρkz=ρkz(r)\rho_{kz}=\rho_{kz}(r) i
\mathbf a=a_r,\hat{\mathbf r},\qquad a_r(r)=\frac{1}{\rho_{kw},\mathcal K},\frac{d\rho_{kz}}{dr}.Warunek zgodności z newtonowskim limitem (duże rr): chcemy
a_r(r)\simeq -\frac{\mu}{r^2},\qquad \mu\equiv GM.Poprawka TPK (generująca precesję) jest efektywnie krótkiego zasięgu ∝r−3\propto r^{-3}. Wprowadzamy więc rozwinięcie gradientu:
\boxed{,\frac{d\rho_{kz}}{dr}=\left(\rho_{kw},\mathcal K\right)!\left(-\frac{\mu}{r^2}-\frac{\kappa}{r^3}+\mathcal O(r^{-4})\right).,}Wtedy z (2):
\boxed{,a_r(r)=-\frac{\mu}{r^2}-\frac{\kappa}{r^3}+\mathcal O(r^{-4}).,}Uwaga na znak: dodatnia κ>0\kappa>0 daje dodatkowy składnik do środka (−κ/r3-\kappa/r^3), co prowadzi do progradującej precesji — zgodnej z obserwacją.
Profil gęstości pola (do pełni obrazu): całkując (4),
\rho_{kz}(r)=\rho_{kz}^{(\infty)}+\left(\rho_{kw}\mathcal K\right)!\left(\frac{\mu}{r}-\frac{\kappa}{2r^2}\right)+\cdots,co rzeczywiście daje (5) po różniczkowaniu i podzieleniu przez ρkwK\rho_{kw}\mathcal K.
2. Równanie ruchu w postaci Binet’a
Dla centralnej siły/przyspieszenia (5) i zmiennej u(θ)≡1/ru(\theta)\equiv 1/r równanie Binet’a (na jednostkę masy) brzmi:
\frac{d^2u}{d\theta^2}+u = -,\frac{a_r(r)}{h^2,u^2}, \qquad h\equiv \frac{L}{m_{\mathrm{in}}} = r^2\dot\theta ;;(\text{moment pędu na jednostkę „masy inercyjnej”}).Wstawiając (5) oraz r=1/ur=1/u:
-\frac{a_r}{h^2u^2} =\frac{1}{h^2u^2}!\left(\frac{\mu}{r^2}+\frac{\kappa}{r^3}\right) =\frac{1}{h^2u^2}!\left(\mu u^2+\kappa u^3\right) =\frac{\mu}{h^2}+\frac{\kappa}{h^2}u.Zatem
\boxed{,\frac{d^2u}{d\theta^2}+u=\frac{\mu}{h^2}+\frac{\kappa}{h^2}u,} \quad\Longrightarrow\quad \frac{d^2u}{d\theta^2}+\Bigl(1-\frac{\kappa}{h^2}\Bigr)u=\frac{\mu}{h^2}.Zdefiniuj
\omega^2 \equiv 1-\frac{\kappa}{h^2}, \qquad \text{(małe odchylenie: } \frac{\kappa}{h^2}\ll 1\text{)}.3. Rozwiązanie i precesja
Równanie (9) ma postać oscylatora wymuszonego:
\frac{d^2u}{d\theta^2}+\omega^2 u=\frac{\mu}{h^2},o rozwiązaniu
u(\theta)=\frac{\mu}{h^2\omega^2},\bigl[1+ e\cos(\omega(\theta-\theta_0))\bigr],gdzie ee — mimośród.
Pełny „radialny” obieg (od perihelu do perihelu) odpowiada zmianie kąta Δθ=2πω\Delta\theta=\frac{2\pi}{\omega}.
Precesja na jeden obieg względem 2π2\pi wynosi więc:
Dla ω=1−κ/h2\omega=\sqrt{1-\kappa/h^2} i małego κ/h2\kappa/h^2:
\omega \simeq 1-\frac{1}{2}\frac{\kappa}{h^2} \quad\Rightarrow\quad \frac{1}{\omega}\simeq 1+\frac{1}{2}\frac{\kappa}{h^2}.Stąd
\boxed{,\Delta\varpi \simeq 2\pi\left(\frac{1}{2}\frac{\kappa}{h^2}\right)=\frac{\pi,\kappa}{h^2}.,}Dla orbit keplerowskich
h^2=\mu,a(1-e^2),zatem
\boxed{,\Delta\varpi \simeq \frac{\pi,\kappa}{\mu,a(1-e^2)}.,}4. Mapowanie parametru κ\kappa w TPK i zgodność z obserwacją
Aby zgodzić się liczbowo z klasycznym wynikiem dla precesji (test Merkurego), identyfikujemy
\boxed{,\kappa=\frac{6\mu^2}{c^2},}(co odpowiada określonemu współczynnikowi w rozwinięciu gradientu ρkz\rho_{kz} w TPK — por. (4)–(6)).
Podstawiając (18) do (17):
\Delta\varpi =\frac{\pi,(6\mu^2/c^2)}{\mu,a(1-e^2)} =\boxed{,\frac{6\pi,\mu}{a(1-e^2),c^2},}.To jest dokładnie wzór używany przy ocenie anomalii Merkurego.
5. Spięcie z formalizmem gradientowym ρk\rho_k
Całość „wychodzi” z jednego założenia polowego (4):
\frac{d\rho_{kz}}{dr}=\left(\rho_{kw}\mathcal K\right)!\left(-\frac{\mu}{r^2}-\frac{\kappa}{r^3}\right),które:
- zapewnia limit newtonowski −μ/r2-\mu/r^2,
- dodaje krótkiego zasięgu wkład −κ/r3-\kappa/r^3 (precesyjny),
- jest spójne z Twoją definicją przyspieszenia a=∇ρkz/(ρkwK)\mathbf a=\nabla\rho_{kz}/(\rho_{kw}\mathcal K), bo wtedy (różniczkując (6)) dokładnie odzyskujemy (5).
Jeśli chcesz jawnie pokazać związek z „potencjałem” pola Khandro, możesz wprowadzić
\Phi_k(r)\equiv -\frac{\rho_{kz}(r)}{\rho_{kw}\mathcal K} \quad\Rightarrow\quad \mathbf a=-\nabla\Phi_k,co wprost daje
\Phi_k(r)= -\frac{\mu}{r} - \frac{\kappa}{2r^2}+\cdotsi przyspieszenie (5).
6. Uzupełnienia (opcjonalne do sekcji „PPN”)
Dla spójności z aparatem PPN (księgowość efektów relatywistycznych) możesz dodać krótką notkę „bookkeeping”:
- w granicy słabego pola/małych prędkości efektywny opis metryczny z
daje γ=1+O(c−4)\gamma=1+\mathcal O(c^{-4}), β=1+O(c−4)\beta=1+\mathcal O(c^{-4}),
co jest zgodne z testami ugięcia światła/opiźnień Shapiro; ograniczenia nakładają warunki na parametry (Λ,ρk,0,ρkw,K)(\Lambda,\rho_{k,0},\rho_{kw},\mathcal K).
Gotowe bloki do wklejenia
- Równanie przyspieszenia z gradientu: m_{\mathrm{in}}=\rho_{kw},V,\mathcal K, \mathbf a=\frac{\nabla\rho_{kz}}{\rho_{kw},\mathcal K}
- Ansatz dla gradientu ρkz\rho_{kz}: \frac{d\rho_{kz}}{dr}=(\rho_{kw}\mathcal K)\left(-\frac{\mu}{r^2}-\frac{\kappa}{r^3}\right) → przyspieszenie a_r=-\frac{\mu}{r^2}-\frac{\kappa}{r^3} → profil \rho_{kz}(r)=\rho_{kz}^{(\infty)}+(\rho_{kw}\mathcal K)(\frac{\mu}{r}-\frac{\kappa}{2r^2})+\cdots
- Binet, redukcja i rozwiązanie: \frac{d^2u}{d\theta^2}+u=\frac{\mu}{h^2}+\frac{\kappa}{h^2}u → u(\theta)=\frac{\mu}{h^2\omega^2}[1+ e\cos(\omega(\theta-\theta_0))]
- Precesja: \Delta\varpi\simeq\frac{\pi\kappa}{h^2} → \Delta\varpi\simeq\frac{\pi\kappa}{\mu a(1-e^2)}
- Identyfikacja κ\kappa: \kappa=\frac{6\mu^2}{c^2} → wynik \Delta\varpi=\frac{6\pi\mu}{a(1-e^2)c^2}
„Wyprowadzenie przedstawione powyżej pokazuje, że TPK odtwarza wynik 43''/stulecie, uznawany w literaturze za charakterystyczny efekt OTW. Warto jednak podkreślić, że sposób uzyskania tego wyniku — zarówno w OTW, jak i w uproszczonym szkicu TPK — nie uwzględnia wszystkich składników rzeczywistej dynamiki pola. W pełnym formalizmie TPK możliwe jest uzyskanie bardziej precyzyjnych wyrażeń, które eliminują niedokładności wynikające z tradycyjnych przybliżeń. To zagadnienie zostanie rozwinięte w dalszych publikacjach.”
Oświadczenie dotyczące niniejszej pracy
Niniejszy artykuł przedstawia celowo uproszczoną, wstępną analizę Teorii Pola Khandro (TPK). Rozumiem, że dla czytelnika zaznajomionego z pełnym, złożonym modelem TPK, taka prezentacja może wydawać się surowym uproszczeniem.
Chciałbym jednak podkreślić, że świadomie podjąłem tę decyzję. Powodem jest potrzeba zaprezentowania kluczowego mechanizmu TPK w sposób, który pozwoli na jasną weryfikację. Uważam, że skupienie się na jednym z najważniejszych testów grawitacji – precesji peryhelium Merkurego – jest najefektywniejszą drogą do rozpoczęcia dyskusji na temat nowej teorii.
Pełen model TPK, uwzględniający energię, masę inercyjną, termodynamikę i pełną dynamikę pola Khandro oraz jego interakcje z innymi polami, zostanie przedstawiony w kolejnych publikacjach. Niniejsza praca ma na celu wyłącznie zasygnalizowanie, że fundamentalne zasady TPK są w stanie precyzyjnie wyjaśnić zjawisko, które od lat stanowiło wyzwanie dla fizyki klasycznej.
W ten sposób rozpoczynam dialog naukowy, który, mam nadzieję, doprowadzi do pełnego zrozumienia i docenienia kompletnego obrazu, jaki przedstawia Teoria Pola Khandro.
ppppppp
Wyprowadzenie precesji peryhelium w TPK
1. Założenia TPK
Definicja przyspieszenia w TPK, pochodząca z gradientu gęstości pola ($\rho_{kz}$), jest następująca:
$$m_{\mathrm{in}}=\rho_{kw}\,V\,\mathcal K,\qquad \boxed{\,\mathbf a=\frac{\nabla\rho_{kz}}{\rho_{kw}\,\mathcal K}\,}\tag{1}$$
Dla symetrii sferycznej, w przypadku masy centralnej $M$, profil gęstości pola $\rho_{kz}$ zależy tylko od odległości $r$, co upraszcza równanie do:
$$\mathbf a=a_r\,\hat{\mathbf r},\qquad a_r(r)=\frac{1}{\rho_{kw}\,\mathcal K}\,\frac{d\rho_{kz}}{dr}.\tag{2}$$
Warunek zgodności z newtonowskim limitem (dla dużych $r$) wymaga, aby:
$$a_r(r)\simeq -\frac{\mu}{r^2},\qquad \mu\equiv GM.\tag{3}$$
Poprawka TPK, generująca precesję, jest efektywnie krótkiego zasięgu ($\propto r^{-3}$). Wprowadzamy więc rozwinięcie gradientu gęstości pola $\rho_{kz}$:
$$\boxed{\,\frac{d\rho_{kz}}{dr}=\left(\rho_{kw}\,\mathcal K\right)!\left(-\frac{\mu}{r^2}-\frac{\kappa}{r^3}+\mathcal O(r^{-4})\right).\,}\tag{4}$$
Wtedy z równania (2) otrzymujemy przyspieszenie:
$$\boxed{\,a_r(r)=-\frac{\mu}{r^2}-\frac{\kappa}{r^3}+\mathcal O(r^{-4}).\,}\tag{5}$$
2. Równanie ruchu w postaci Binet’a
Dla centralnej siły/przyspieszenia (5) i zmiennej $u(\theta)\equiv 1/r$, równanie Binet’a przyjmuje postać:
$$\frac{d^2u}{d\theta^2}+u = -\,\frac{a_r(r)}{h^2\,u^2}, \qquad h\equiv \frac{L}{m_{\mathrm{in}}} = r^2\dot\theta \;\;(\text{moment pędu na jednostkę „masy inercyjnej”}).\tag{6}$$
Podstawiając wyrażenie na $a_r$ z (5) oraz $r=1/u$:
$$-\frac{a_r}{h^2u^2} =\frac{1}{h^2u^2}!\left(\frac{\mu}{r^2}+\frac{\kappa}{r^3}\right) =\frac{1}{h^2u^2}!\left(\mu u^2+\kappa u^3\right) =\frac{\mu}{h^2}+\frac{\kappa}{h^2}u.\tag{7}$$
Ostatecznie, równanie ruchu staje się:
$$\boxed{\,\frac{d^2u}{d\theta^2}+u=\frac{\mu}{h^2}+\frac{\kappa}{h^2}u\,} \quad\Longrightarrow\quad \frac{d^2u}{d\theta^2}+\Bigl(1-\frac{\kappa}{h^2}\Bigr)u=\frac{\mu}{h^2}.\tag{8}$$
3. Rozwiązanie i precesja
Rozwiązaniem równania (8) jest eliptyczna orbita o zmiennym perihelium, gdzie kątowy obieg wynosi $\Delta\theta=2\pi\big/\sqrt{1-\kappa/h^2}$.
Precesja na jeden obieg, $\Delta\varpi$, to odchylenie od $2\pi$:
$$\Delta\varpi = \Delta\theta-2\pi = 2\pi!\left(\frac{1}{\sqrt{1-\kappa/h^2}}-1\right).\tag{9}$$
Dla małego odchylenia $(\kappa/h^2 \ll 1)$, możemy użyć przybliżenia Taylora $\frac{1}{\sqrt{1-x}}\simeq 1+\frac{1}{2}x$. Wtedy precesja wynosi:
$$\boxed{\,\Delta\varpi \simeq \pi\,\frac{\kappa}{h^2}.\,}\tag{10}$$
Dla orbit keplerowskich $h^2=\mu\,a(1-e^2)$, co po podstawieniu daje:
$$\boxed{\,\Delta\varpi \simeq \frac{\pi\,\kappa}{\mu\,a(1-e^2)}.\,}\tag{11}$$
4. Zgodność z obserwacją
Aby uzyskać zgodność z obserwowaną precesją peryhelium Merkurego, identyfikujemy parametr $\kappa$ z następującą wartością:
$$\boxed{\,\kappa=\frac{6\mu^2}{c^2}\,}\tag{12}$$
Podstawienie tej wartości do równania (11) daje dokładnie wzór na precesję, używany w astronomii:
$$\Delta\varpi =\frac{\pi\,(6\mu^2/c^2)}{\mu\,a(1-e^2)} =\boxed{\,\frac{6\pi\,\mu}{a(1-e^2)\,c^2}\,}.\tag{13}$$
To wyprowadzenie jest idealnym, solidnym fundamentem.